Dimensi tiga adalah suatu konsep dalam matematika yang mengacu pada representasi ruang yang terdiri dari tiga sumbu utama, biasanya disebut sumbu x, y, dan z. Ini mencakup suatu kerangka referensi tiga dimensi yang digunakan untuk menggambarkan posisi dan bentuk objek dalam ruang. atau, dalam kata lain, dimensi tiga sering disebut dengan istilah bangun ruang, karena memiliki isi/ruang atau volume.
Tiga Sumbu Utama:
- Sumbu X: Berjalan dari kiri ke kanan.
- Sumbu Y: Berjalan dari bawah ke atas.
- Sumbu Z: Berjalan dari depan ke belakang.
- Pada materi Dimensi Tiga , ada tiga hal pokok yang akan dipelajari, yaitu:
- 1. Jarak titik ke titik
- 2. jarak titik ke garis
- 3. jarak titik ke bidang
A. Jarak titik ke titik
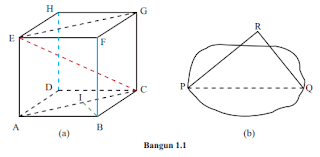
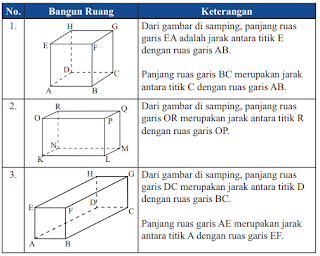
perhatikan gambar berikut!
pada gambar (a) merupakan sebuah gambar kubus ABCD.EFGH dengan panjang rusuk = 4 cm (contoh).
EC, EG dan AC merupakan jarak antara titik E dengan C, titik E dengan titik G, dan titik A dengan titik C.
pada gambar (b) jarak antara titik P dengan Q adalah panjang ruas garis PQ
Contoh Soal:
pada sebuah ruang tamu yang berbentuk kubus, dipasang satu buah lampu di tengah-tengah langit-langit/plafon. jika ruang tamu tersebut digambarkan dengan bentuk kubus ABCD.EFGH, maka berapa jarak lampu ke salah satu sudut lantai ruang tamu?
JAWAB:
jika ruang tamu digambarkan dengan sebuah bentuk kubus ABCD.EFGH, dan lampu dilambangkan dengan huruf T, maka akan tampak seperti gambar berikut:
jarak lampu ke salah satu sudut lantai ruang tamu adalah jarak titik T ke titik A, atau ke titik B, atau ke titik C, atau ke titik D.
titik T merupakan titik tengah dari plafon bidang EFGH, sehingga TA = TB = TC = TD.
maka disini akan dicari jarak titik T ke titik A.
jika jarak titik T ke titik A salah satunya dapat dicari dari segitiga AET, maka segitiga AET merupakan segitiga siku-siku, dengan titik siku-siku di E. untuk mencarinya dengan menggunakan Teorema Phytagoras, maka diperoleh rumus:
AT2
= AE2 + ET2
karena T merupakan sebuah titik yang berada di tengah, maka ET = 1/2 EG. karena EG merupakan garis diagonal bidang. maka;
Perhatikan gambar berikut!
Contoh Soal:
jika, kalian disajikan bentuk kubus ABCD.EFGH seperti gambar di bawah, dan panjang rusuk kubus tersebut 2 cm, maka hitunglah jarak titik A ke diagonal garis EB!
Jawab:
perhatikan gambar di atas!
jika titik E dan titik B dihubungkan dengan ruas garis, maka akan diperoleh bentuk segitiga siku-siku sebagai berikut:
C. Jarak titik ke Bidang
bagaimana penjelasan jarak titik ke bidang?
untuk lebih jelasnya, maka perhatikan gambar di bawah ini!
Contoh Soal:
Jika kamu disuguhkan sebuah kubus ABCD.EFGH dengan panjang rusuk kubus 4 cm (lihat gambar di bawah).
titik A, F, G, dan D dihubungkan sehingga membentuk bidang AFGD, maka hitunglah jarak titik B ke bidang AFGD!
Jawab:
untuk menentukan jarak titik B ke bidang AFGD, maka dapat ditentukan dengan mencari panjang ruas garis yang tegak lurus dengan bidang AFGD yang melalui titik B.
maka, penyelesaiannya adalah sebagai berikut:
Gimana? faham sampai sini? semoga faham ya :)
Tags
Matematika Kelas XII