Barisan dan Deret Aritmetika

Konsep Barisan dan Deret

    Barisan dan deret dalam matematika memiliki manfaat yang banyak dalam kehidupan sehari-hari. Misalnya Ketika kamu ingin menjadi seorang pengusaha, perkembangan usaha yang konstan dari waktu ke waktu mengikuti baris hitung. Kamu jadi bisa memprediksikan skala keuntungan atau kerugian yang akan kamu hadapi.

Secara umum, barisan adalah sebuah daftar bilangan yang mengurut dari kiri ke kanan. Setiap urutan bilangannya juga memiliki karakteristik atau pola tertentu. Setiap bilangan yang ada pada barisan merupakan suku dalam barisan itu sendiri.

Sementara itu, deret adalah penjumlahan suku-suku dari suatu barisan. Misalnya, terdapat barisan U₁, U₂, U₃, U₄, ….. U_n, maka deret itu adalah U₁ + U₂ + U₃ + U₄ +….. U_n. Oh iya, “U” itu artinya suku ya. Kalau U_n berarti suku ke-n.

Lalu, apa sih yang dimaksud dengan barisan dan deret aritmetika?

 

Pengertian Barisan dan Deret Aritmetika

Sejatinya, materi barisan dan deret aritmetika sudah pernah kamu pelajari di kelas 8 SMP/MTs. baca => ‘Bedanya Rumus Barisan dan Deret Aritmetika beserta Contoh Soalnya.

Aritmetika dapat diartikan sebagai ilmu hitung dasar dalam matematika yang mencakup penjumlahan, pengurangan, pembagian, juga perkalian. Kamu harus ingat, nih, penyebutan yang betul adalah ‘aritmetika’, bukan aritmatika!

Kalau kita lihat pada bentuk barisan, jika selisih antara suku ke-1 dengan suku ke-2, dan seterusnya sama, maka dapat disebut barisan aritmetika.

Dengan kata lain, barisan aritmetika adalah barisan bilangan yang memiliki selisih yang sama di antara suku-sukunya yang saling berdekatan. Selisih ini bisa kita sebut dengan beda, simbolnya b, ya. Kalau deret aritmetika adalah jumlah suku ke-n pertama pada barisan aritmatika.

Misalnya, di suatu barisan memiliki suku pertama, yaitu 1. Suku pertama barisan aritmetika disimbolkan dengan U₁ atau a. Lalu, di suku kedua (U₂), yaitu 4. Suku ketiga (U₃), yaitu 7, suku keempat (U₄), yaitu 10, dan seterusnya. Berarti, barisan ini memiliki beda, yaitu 3 pada setiap sukunya.

Rumus Barisan dan Deret Aritmetika beserta Contoh

Sekarang, kita pahami rumusnya. Rumus barisan aritmetika bisa kamu gunakan untuk mencari suku ke-n (U_n). Sementara itu, rumus deret aritmetika berguna untuk mencari penjumlahan dari suku-suku tersebut.

Oke, supaya kamu lebih mudah memahami rumusnya, kita langsung masuk ke contoh soal saja. Misalnya terdapat barisan bilangan 1, 3, 5, 7, 9, 11, … Maka,

Suku pertama = U₁ = a = 1

Suku kedua = U₂ = 3

Suku ketiga = U₃ = 5 … dst sampai suku ke-n = U_n

Beda atau selisih suku pertama dengan suku kedua, suku kedua dengan suku ketiga, dan seterusnya:

b = U₂ – U₁ = 3 – 1 = 2

b = U₃ – U₂ = 5 – 3 = 2

b = U₄ – U₃ = 7 – 5 = 2 … dst

Jadi, b = 2.

Kita diminta mencari suku ke-n (U_n) dari barisan bilangan tadi. Kalau semisal yang ditanya adalah suku ke-7 (U₇), caranya gampang ya, gais. Kamu tinggal tambahkan saja suku ke-6 (U₆) dengan nilai beda nya.

b = U₇ – U₆

U₇ = U₆ + b

U₇ = 11 + 2 = 13

Tapi, bagaimana jika kita diminta untuk mencari suku ke-20, atau suku ke-35, atau suku ke-100? Sangat nggak efektif kalau kita jumlahkan satu per satu tiap suku dengan beda nya, ya. Oleh karena itu, kita membutuhkan rumus barisan aritmetika.

 Sekarang, coba kita cari suku ke-20 menggunakan rumus di atas, ya!

Un = a + (n – 1)b

U20 = 1 + (20 – 1)2

U20 = 1 + (19.2)

U20 = 1 + 38 = 39

Jadi, suku ke-20 barisan aritmetika tersebut adalah 39. gampang kan? faham sampai sini?

Contoh:

Terdapat barisan aritmetika 3, 6, 9, 12, …, 81

1. Tentukan nilai suku tengah dari barisan aritmetika tersebut!
2. Tentukan suku ke berapakah yang menjadi suku tengah dari barisan aritmetika tersebut!

 

Penyelesaian:

Diketahui:

a = 3

b = U2 – U1 = 6 – 3 = 3

Un = 81  

Ditanya: Ut dan t …?

Jawab:

a. Ut

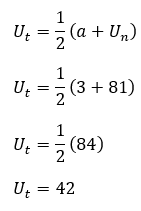
Jadi, nilai suku tengah pada barisan aritmetika di atas adalah 42.

b. t

 

Jadi, suku ke-14 adalah suku tengah dari barisan aritmetika di atas

Rumus Sisipan Barisan Aritmetika

Kalau tadi kan kasusnya kita mau mencari nilai suku tengah pada suatu barisan aritmetika, nah Gimana kalau sekarang kasusnya kita ubah!? 

Misalnya, kita akan menyisipkan sejumlah bilangan ke dalam barisan aritmetika yang sudah ada. Pastinya, hal ini akan menyebabkan terbentuknya barisan aritmetika baru dong, ya. 

Contoh:

Kita punya barisan aritmetika sebagai berikut:

1, 9, 17

Barisan tersebut memiliki banyak suku n = 3 dan beda b = 8. Kemudian, kita sisipkan 6 buah bilangan ke dalam barisan aritmetika di atas, sehingga:

1, 3, 5, 7, 9, 11, 13, 15, 17

Jadi, terbentuklah barisan aritmetika baru dengan banyak suku n’ = 9 dan beda b’ = 2.

Sampai sini paham? 

Contoh:

Di antara bilangan 20 dan 116 disisipkan 11 bilangan, sehingga terbentuklah barisan aritmetika baru. Tentukan:

1. Beda barisan aritmetika baru
2. Suku tengah barisan artimetika baru dan letaknya
3. Suku ke-10 dari barisan aritmatika baru

 

Pembahasan:

Diketahui:

a = a’ = 20

b = 116 – 20 = 96

k = 11

Un = Un’ = 116

n’ = k + n = 11 + 2 = 13

Ditanya: b’, Ut‘, U10‘ …?

Jawab:

a. b’

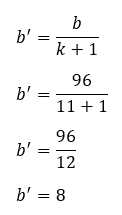
Jadi, nilai beda pada barisan aritmetika baru adalah 8.

b. Ut‘

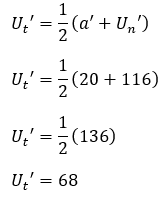
Jadi, suku tengah pada barisan aritmetika baru adalah 68.

c. U10‘

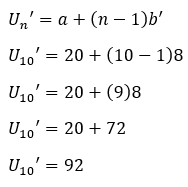
Jadi, suku ke-10 pada barisan aritmetika baru adalah 92.

gimana gimana? sampai sini paham gak? semoga paham ya